Which of the following is the total number of whole boxes that measure 2.4 ft * 2.4 ft * 2.4 ft that can be stored in a room that measures 18 ft * 18 ft * 18 ft, if the size of the boxes cannot be altered?
125
92
422
400
Correct Answer : C
The number of boxes is determined by finding the volume of the room divided by the volume of the box.
Number of boxes
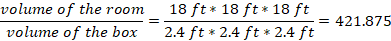
The number of boxes that can be stored in the room is about 422.
TEAS 7 Exam Quiz Bank
HESI A2 Exam Quiz Bank
Find More Questions 📚
Teas 7 Questions: We got the latest updated TEAS 7 questions
100% Money Refund: 100% money back guarantee if you take our full
assessment pass with 80% and fail the actual exam.
Live Tutoring: Fully customized live tutoring lessons.
Guaranteed A Grade: All students who use our services pass with 90%
guarantee.
Related Questions
Correct Answer is C
Explanation
The number of boxes is determined by finding the volume of the room divided by the volume of the box.
Number of boxes
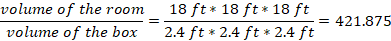
The number of boxes that can be stored in the room is about 422.
Correct Answer is D
No explanation
Correct Answer is D
Explanation
We need to find the circumference of the circle.
Before finding the circumference of a circle, we need to find the radius of the circle from the given area.
Let r be the radius of the circle, then the area of the circle is:
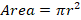
Substituting the value of area in the above equation
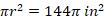
Dividing both sides by pi and taking square root on both sides yields
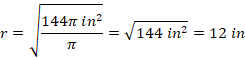
The radius of the circle with the given area is 12 in, and the circumference of the circle becomes:
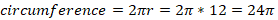
Correct Answer is C
Explanation
To find the circumference of the circle, we start by using the formula for the area of a circle:
\(A=πr2A = \pi r^2A=πr2\)
The given area is 36π36\pi36π. Setting the two equal:
\(πr2=36π\pi r^2 = 36\piπr2=36π\)
Dividing both sides by π\piπ:
\(r2=36r^2 = 36r2=36\)
Taking the square root of both sides:
\(r=6r = 6r=6\)
Now, we use the formula for the circumference of a circle:
\(C=2πrC = 2\pi rC=2πr\)
Substituting r=6r = 6r=6:
\(C=2π×6=12π inC = 2\pi \times 6 = 12\pi \, \text{in}C=2π×6=12πin\)
The correct answer is:
c. 12 \pi in
This question was extracted from the actual TEAS Exam. Ace your TEAS exam with the actual TEAS 7 questions, Start your journey with us today
Visit Naxlex, the Most Trusted TEAS TEST Platform With Guaranteed Pass of 90%.
Money back guarantee if you use our service and fail the actual exam. Option of personalised live tutor on your area of weakness.
